Generating All Bitsets
Posted: December 16, 2020 Filed under: Bit twiddling, C++ Leave a commentHere’s a simple trick for iterating through all bitstrings with bits set only at certain positions (specified by a mask):
#include <cstdint>
#include <cstdlib>
#include <iostream>
#include <bitset>
typedef uint16_t T;
T nextbitset(T n, T mask) {
n |= ~mask; // Set all bits not in the mask
n += 1; // Increment
n &= mask; // Clear all bits not in the mask
return n;
}
int main(int argc, char *argv[]) {
T mask = strtoul(argv[1],0,2), n = 0; // Read in binary
do {
std::cout << std::bitset<8*sizeof(T)>(n) << "\n";
n = nextbitset(n,mask);
} while (n);
}
$ g++ -Wall bitset.cpp -o bitset
$ ./bitset 100011
0000000000000000
0000000000000001
0000000000000010
0000000000000011
0000000000100000
0000000000100001
0000000000100010
0000000000100011
tolower
Posted: February 12, 2014 Filed under: Bit twiddling, C Leave a commentIn an Age of Highly Pipelined RISC Architectures, we might be tempted to write a basic ASCII lower-case function as:
int tolower1(int c)
{
return c|-(c-0101U<032)&040;
}
and avoid any branching. We subtract ‘A’ from c and do an unsigned comparison with ‘Z’-‘A’, convert to a bitmask and use that to ‘or’ in the lower case bit where necessary.
A more quiche-eating approach would be the clear and obvious:
int tolower2(int c)
{
if (c >='A' && c <= 'Z') return c+'a'-'A';
else return c;
}
at which hard-nosed hacker types will sneer, however, an Age of Highly Pipelined RISC Architectures is also an Age of Conditional Move Instructions, and GCC generates the pleasantly concise:
tolower2: leal -65(%rdi), %ecx leal 32(%rdi), %edx movl %edi, %eax cmpl $25, %ecx cmovbe %edx, %eax ret
for our simple approach rather than the distinctly bloated:
tolower1: leal -65(%rdi), %eax cmpl $25, %eax setbe %al movzbl %al, %eax negl %eax andl $32, %eax orl %edi, %eax ret
All is not lost though for the hard-nosed hacker, for this is also an Age of Vectorization and we can do something similar using SSE2 instructions to lower-case not one but 16 characters at a time:
#include <x86intrin.h>
void tolower128(char *p)
{
__m128i v1 = _mm_loadu_si128((__m128i*)p);
__m128i v2 = _mm_cmplt_epi8(v1,_mm_set1_epi8('A'));
__m128i v3 = _mm_cmpgt_epi8(v1,_mm_set1_epi8('Z'));
__m128i v4 = _mm_or_si128(v2,v3);
__m128i v5 = _mm_andnot_si128(v4,_mm_set1_epi8(0x20));
_mm_storeu_si128((__m128i*)p, _mm_or_si128(v1,v5));
}
Now everyone should be happy!
Inverse Square Root II
Posted: November 25, 2012 Filed under: Bit twiddling, Floating Point Leave a commentHmmm, after writing that rather long and laborious post about the bit-level interpretation of fast inverse square root, I came across a couple of excellent blog posts by Christian Plesner Hansen:
http://blog.quenta.org/2012/09/0x5f3759df.html
http://blog.quenta.org/2012/09/0x5f3759df-appendix.html
which got me thinking about all this again (it’s a real mind-worm this one)…
So, now the scales have dropped from my eyes, let’s try again: what we are really doing is using a rough approximation to log2(n), represented as a fixed point number, that happens to be easily computed from the floating point representation. Once we have our approximate log (and exp) function, we can do the the usual computations of roots etc. using normal arithmetic operations on our fixed point representation, before converting back to a float using our exp function.
So, take a number, 2n(1+m) where 0<=m<1, a reasonable approximation to log2(x) is n+m, and we can improve the approximation by adding a small constant offset, σ and, because we are doing this in the fixed point realm, everything works out nicely when we convert back to the floating point realm. Here is a picture for n=0, choosing by eye a value of σ = 0.045:
Now, if interpret a non-negative IEEE-754 float 2n(1+m) as a 9.23 fixed point value (ie. with 9 bits to the left of the binary point, 23 bits to the right), then this fixed point number is (e+m), where e = n+127, and, as above, this is approximates log2(2e(1+m)), so e-127+m = n+m is an approximation to log2(2e-127(1+m)) = log2(2n(1+m)), ie. log2 of our original number. Note that e+m is always positive, but e+m-127 may not be, so might need to be represented as a signed value.
As far as actual code goes, first we need to be able to get at the bitwise representation of floats. It’s nice to avoid aliasing issues etc. by using memcpy; my compiler (gcc 4.4.3) at least generates sensible code for this:
static inline float inttofloat(uint32_t n)
{
float f;
memcpy(&f,&n,sizeof(f));
return f;
}
static inline uint32_t floattoint(float f)
{
uint32_t n;
memcpy(&n,&f,sizeof(n));
return n;
}
We are working in our fixed point representation, so adding 127 is actually done by adding 127<<23 = 0x3f800000 and we convert our σ offset in the same way:
uint32_t sigma = 45*(uint32_t(1)<<23)/1000;
uint32_t c = (uint32_t(127)<<23) - sigma;
int32_t alog(float x) {
return floattoint(x)-c;
}
We also want an inverse of our approximate log, ie. an approximate exp, but this is just a reverse of the previous step:
float aexp(int32_t n) {
return inttofloat(n+c);
}
Provided we haven’t left the realm of representable floats, the sign bit of the result should alway be zero.
We can use our log approximation directly as well of course, to convert from fixed point we need:
float unfix(int32_t n) {
return float(n)/(1<<23);
}
float unfix(uint32_t n) {
return float(n)/(1<<23);
}
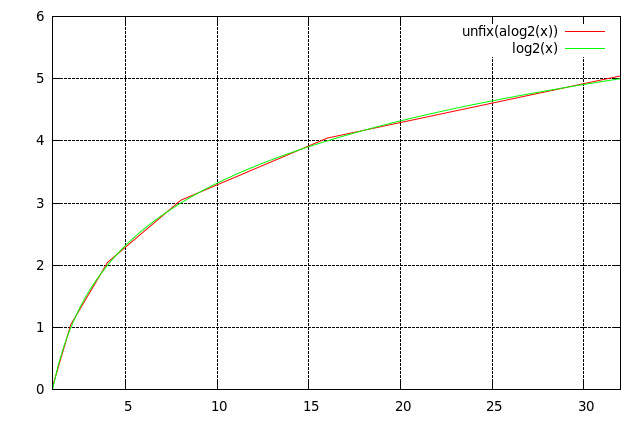
Another nice picture, showing our log2 approximation over a wider range:
Now we can define:
float sqrt(float x) { return aexp(alog(x)/2); }
float invsqrt(float x) { return aexp(alog(x)/-2); }
float cubert(float x) { return aexp(alog(x)/3); }
and so on.
To relate this to the original magic function, for an inverse square root, the integer manipulations are:
invsqrt(n) = -((n-c)/2) + c
= -(n/2 - c/2) + c // Not exact, but close enough
= c/2 - n/2 + c
= -(n>>1) + ((c>>1) + c)
Calculating (c>>1) + c we get 0x5f375c29, satisfyingly close to the original magic constant 0x5f3759df…
We can use signed or unsigned fixed point numbers for our logs, the arithmetic will be the same, providing we can avoid overflow, so for example, if to get an approximate value for log(factorial(50)), we can do:
uint32_t fact = 0;
for (int i = 1; i <= 50; i++) {
fact += alog(i);
}
printf("%g\n", unfix(fact));
giving the result 213.844, comparing nicely to the true result of 214.208. Note that if I were to have used a signed value for fact, the result would have overflowed.
Be warned, this is only a very rough approximation to the log2 function, only use it if a very crude estimate is good enough, or if you are going do some further refinement of the value. Alternatively, your FPU almost certainly uses some variation of this technique to calculate logs (or at least an initial approximation) so you could just leave it to get on with it.
Like many things, this isn’t particularly new, the standard reference is:
J. N. Mitchell, “Computer multiplication and division using binary logarithms,” IRE Trans. Electron. Computers, vol. 11, pp. 512–517, Aug. 1962
Fast inverse square root
Posted: November 19, 2012 Filed under: Bit twiddling, C++, Floating Point 2 CommentsWhat could be cuter than the infamous fast inverse square root function used in the Quake 3 engine:
http://en.wikipedia.org/wiki/Fast_inverse_square_root
The interesting part is the calculation of the initial approximation, splitting this down into the basic steps, we have:
float isqrt(float f)
{
uint32_t n = floattoint(f);
n >>= 1;
n = -n;
n += 0x5f000000;
n += 0x3759df;
float x = inttofloat(n);
return x;
}
To get some insight into what’s going on here, we need to look at the representation of floating point numbers. An IEEE-754 float consists of a sign bit, an exponent value, and a mantissa. The exponent is an 8-bit value, the mantissa has 23 bits, both unsigned. As usual, a suitable notation is key: simplifying a little (specifically, ignoring NaNs, infinities and denormalized numbers), we shall write a float of the form {sign:1;exponent:8;mantissa:23} as (s,e,m), with m a real in the range [0,1), and this represents 2e-127(1+m), negated if the sign bit is 1.
To warm up, it’s helpful to look at a simpler example:
float fsqrt(float f)
{
unsigned n = floattoint(f);
n >>=1;
n += 0x1f800000;
n += 0x400000;
return inttofloat(n);
}
Here we are computing an approximation to a normal square root.
Taking it a step at a time: first the shift right n >>= 1, there are two cases for odd and even exponent:
(0,2e,m) => (0,e,m/2) // No carry from exponent (0,2e+1,m) => (0,e,1/2 + m/2) // Carry into mantissa
For n += 0x1f800000: we are adding 63 (0x1f800000 is 63 << 23) onto the exponent:
(s,e,m) => (s,e+63,m)
And finally, n += 0x400000: Generally, if we add p onto the mantissa, where 0 <= p < 223, and writing m’ = m + p/223, we have:
(s,e,m) => (s,e,m') if m' < 1 (s,e,m) => (s,e+1,m'-1) if m' >= 1
For p = 0x400000 = 222, we have m' = m+1/2. ie:
(s,e,m) => (s,e+1,m'-1) if m' >= 1
=> (s,e,m') otherwise
Putting this together, for even powers of two:
22k(1+m) => 2k(1+m/2):
(0,2k+127,m) => (0,k+63,0.5+m/2)
=> (0,k+126,0.5+m/2)
=> (0,k+127,m/2)
And for odd powers:
2(2k+1)(1+m) => 2k(1+0.5+m/2):
(0,2k+1+127,m) => (0,k+64,m/2)
=> (0,k+127,m/2)
=> (0,k+127,0.5+m/2)
Let’s check this is sensible by setting m = 0:
22k => 2k 2(2k+1) => 2k(1+0.5)
and putting m = 1 we get:
22k+1 => 2k(1+1/2) 2(2k+2) => 2k+1
Our approximation is linear in between powers of two, and continuous at those points too. Also at even powers the graph is tangent to sqrt(x).
This is all nicely illustrated in a picture:
Returning to the original inverse function, we have an additional negation step, n = -n: to negate a twos-complement number, we flip the bits and add one. There are two main cases, depending on whether the mantissa is zero. If it is zero, there is a carry into the exponent, otherwise we just flip the bits of the exponent. The sign bit will always end up set (I’m ignoring the case when the exponent is zero). The general effect is:
(0,e,0) => (1,256-e,0) (0,e,m) => (1,255-e,1-m)
This time, we are adding 190 onto the exponent (0x5f000000 = 190<<23) – this has the dual effect of resetting the sign bit to 0 and subtracting 66 from the exponent (190 = -66 mod 256).
Let’s see what happens with odd and even powers of two; writing the magic offset added onto the mantissa as c:
(0,2k+127,m) => (0,k+63,0.5+m/2) // n >>= 1
=> (1,255-k-63,0.5-m/2) // n = -n
=> (0,126-k,0.5-m/2) // n += 0x5f000000
=> (0,126-k,0.5-m/2+c) // if 0.5-m/2+c < 1
=> (0,127-k,-0.5-m/2+c) // if 0.5-m/2+c >= 1
(0,2k+128,m) => (0,k+63,m/2) // n >>= 1
=> (1,255-k-63,1-m/2) // n = -n
=> (0,126-k,1-m/2) // n += 0x5f000000
=> (0,126-k,1-m/2+c) // if 1-m/2+c < 1
=> (0,127-k,-m/2+c) // if 1-m/2+c >= 1
If we use 0x400000 as the offset, ie. c above is 0.5, and put m=0 in the two cases, we have:
22k => 1/2k 22k+1 => 1.5/2k+1
Once again, our approximation coincides exactly at even powers of two, and as before it’s useful to have a picture:
We don’t have nice tangents this time, but the end result isn’t too bad.
We probably could have saved ourselves some work here by noting that the mapping between 32-bit integers (as signed magnitude numbers) and the corresponding floats is monotonic and continuous (for some sense of continuous), so composing with other (anti)monotonic operations gives an (anti)monotonic result, so having checked our function is correct at powers of two, it can’t go too badly adrift in between.
We can improve our approximation by using a smaller mantissa offset, 0x3759df, and we end up with the function we came in with:
Not especially pretty, but a good starting point for some Newton-Raphson. Notice that as well as kinks at exact powers of two, this approximation has kinks in between as well (when adding the constant to the mantissa overflows into the exponent).
Reversing a 64-bit word
Posted: November 18, 2012 Filed under: Bit twiddling Leave a commentHere’s a cute way of reversing a 64-bit word (there is a similar, slightly faster, but slightly more obscure method in TAOCP 4a, so if you really need to save the cycles, use that one).
We use ternary swaps: for example, to bit-reverse a 3-bit sequence, we can just swap the high and low bits. To bit-reverse a 9-bit segment, break into [3,3,3] and swap the top and bottom 3-bit sections, and then bit-reverse each 3-bit section separately.
More generally, we can reverse any bit sequence by breaking it up into [M,N,M], swapping top and bottom sections (by shifting up and down by M+N), and recursing.
So, to reverse a 63 bit number, since 63 = 3*3*7, we can nest two 3-swaps and a 7-swap. We can do the actual swapping of sections with another classy Knuth function, nicely expressible as a C++ template:
template <typename T, T m, int k>
static inline T swapbits(T p) {
T q = ((p>>k)^p)&m;
return p^q^(q<<k);
}
m is a mask, k a shift amount, the function swaps the bits at positions given by the set bits of m and m<<k (clearly these two should be disjoint, ie. m & m<<k == 0)
All we need to do now is calculate the masks and the shift amounts.
First 3-swap; the binary mask is ...001001001 and we need to shift the mask up by 2. We can see that m1 + m1<<1 + m1<<2 = 2^63-1, so we can calculate the mask with a (compile-time) division.
Second 3-swap: the binary mask is ...000000111000000111 and we need to shift the mask up by 6. Once again, we can easily compute the correct mask.
The 7-swap (ie. reverse 7 sections of 9 bits), we do in two stages, do a 3-swap for the top and bottom sections, so the mask is 111111111 + 111111111<<36, finally we swap the top and bottom 27 bits, so the mask is just 2^27-1, and the shift is 36.
This reverses the bottom 63 bits, a simple rotate by one then puts everything into the right place.
uint64_t bitreverse (uint64_t n)
{
static const uint64_t m1 = ((uint64_t(1)<<63)-1)/(1+(1<<1)+(1<<2));
static const uint64_t m2 = ((uint64_t(1)<<63)-1)/(1+(1<<3)+(1<<6));
static const uint64_t m3 = ((uint64_t(1)<<9)-1)+(((uint64_t(1)<<9)-1)<<36);
static const uint64_t m4 = (uint64_t(1)<<27)-1;
n = swapbits<uint64_t, m1, 2>(n);
n = swapbits<uint64_t, m2, 6>(n);
n = swapbits<uint64_t, m3, 18>(n);
n = swapbits<uint64_t, m4, 36>(n);
n = (n >> 63) | (n << 1);
return n;
}
Here is what gcc makes of that:
_Z10bitreversey: movq %rdi, %rdx movabsq $1317624576693539401, %rax movabsq $126347562148695559, %rcx shrq $2, %rdx xorq %rdi, %rdx andq %rax, %rdx movq %rdx, %rax salq $2, %rdx xorq %rdi, %rax xorq %rdx, %rax movq %rax, %rdx shrq $6, %rdx xorq %rax, %rdx andq %rcx, %rdx movabsq $35115652612607, %rcx xorq %rdx, %rax salq $6, %rdx xorq %rdx, %rax movq %rax, %rdx shrq $18, %rdx xorq %rax, %rdx andq %rcx, %rdx xorq %rdx, %rax salq $18, %rdx xorq %rdx, %rax movq %rax, %rdx shrq $36, %rdx xorq %rax, %rdx andl $134217727, %edx xorq %rdx, %rax salq $36, %rdx xorq %rdx, %rax rorq $63, %rax ret
For comparison, here is Knuth’s 64-bit reverse (I’ve just hard-coded the constants this time). It’s based on a 32-bit reverse that breaks one 17-bit segment into [7,3,7] and the remaining 15-bit segment into [3,7,3] – we can do both swaps with the same shift of 10. First step is to swap adjacent bits which can be done slightly faster than a general swap. Very cunning:
uint64_t kbitreverse (uint64_t n)
{
static const uint64_t m0 = 0x5555555555555555LLU;
static const uint64_t m1 = 0x0300c0303030c303LLU;
static const uint64_t m2 = 0x00c0300c03f0003fLLU;
static const uint64_t m3 = 0x00000ffc00003fffLLU;
n = ((n>>1)&m0) | (n&m0)<<1;
n = swapbits<uint64_t, m1, 4>(n);
n = swapbits<uint64_t, m2, 8>(n);
n = swapbits<uint64_t, m3, 20>(n);
n = (n >> 34) | (n << 30);
return n;
}
and the corresponding compiler output:
_Z11kbitreversey: movq %rdi, %rdx movabsq $6148914691236517205, %rax movabsq $216384095313249027, %rcx shrq %rdx andq %rax, %rdx andq %rdi, %rax addq %rax, %rax orq %rdx, %rax movq %rax, %rdx shrq $4, %rdx xorq %rax, %rdx andq %rcx, %rdx movabsq $54096023692247103, %rcx xorq %rdx, %rax salq $4, %rdx xorq %rdx, %rax movq %rax, %rdx shrq $8, %rdx xorq %rax, %rdx andq %rcx, %rdx movabsq $17575006191615, %rcx xorq %rdx, %rax salq $8, %rdx xorq %rdx, %rax movq %rax, %rdx shrq $20, %rdx xorq %rax, %rdx andq %rcx, %rdx xorq %rdx, %rax salq $20, %rdx xorq %rdx, %rax rorq $34, %rax ret
Knuth wins here by 1 instruction! Oh well, maybe I’ll have better luck next time…
Templated bit twiddling
Posted: October 6, 2012 Filed under: Bit twiddling Leave a commentSometimes it’s nice to combine C++ template metaprogramming with some bit twiddling, here’s a classic parallelized bit counting algorithm with all the magic numbers constructed as part of template instantiation:
#include <stdio.h>
#include <stdlib.h>
template <typename T, int k, T m>
struct A
{
static T f(T n)
{
static const int k1 = k/2;
n = A<T, k1, m^(m<<k1)>::f(n);
return ((n>>k)&m) + (n&m);
}
};
template <typename T, T m>
struct A<T, 0, m>
{
static T f(T n) { return n; }
};
template<typename T>
static inline int bitcount (T n)
{
static const int k = 4 * sizeof(n);
return A<T, k, (T(1)<<k)-1>::f(n);
}
int main(int argc, char *argv[])
{
unsigned long n = strtoul(argv[1], NULL, 10);
printf("bitcount(%lu) = %d\n", n, bitcount(n));
}
We could extract the magic number construction out as a separate template, and there are some extra optimizations that this code doesn’t do, for example, the level 1 code can be simplified to:
i = i - ((i >> 1) & 0x55555555);
rather than what we get from the above:
i = ((i >> 1)&0x55555555) + (i&0x55555555);
Adding an appropriate partial template instantiation for A<T,1,m> is left as an exercise.
In fact, there are lots of shortcuts that can be made here, we aren’t really being competitive with Bit Twiddling Hacks:
unsigned int v; // count bits set in this (32-bit value)
unsigned int c; // store the total here
static const int S[] = {1, 2, 4, 8, 16}; // Magic Binary Numbers
static const int B[] = {0x55555555, 0x33333333, 0x0F0F0F0F, 0x00FF00FF, 0x0000FFFF};
c = v - ((v >> 1) & B[0]);
c = ((c >> S[1]) & B[1]) + (c & B[1]);
c = ((c >> S[2]) + c) & B[2];
c = ((c >> S[3]) + c) & B[3];
c = ((c >> S[4]) + c) & B[4];
which would need 3 template specializations and we are starting to get a bit complicated…
In the same style then, here’s a bit reverse function, with a separate magic number calculating template:
#include <stdio.h>
#include <stdlib.h>
template <typename T, int k>
struct Magic {
static const T m = ~T(0)/(T(1)+(T(1)<<k));
};
template <typename T, int k>
struct RevAux {
static inline T f(T n) {
T n1 = RevAux<T,k/2>::f(n);
return ((n1>>k) & Magic<T,k>::m) | ((n1 & Magic<T,k>::m)<<k);
}
};
template <typename T>
struct RevAux<T,0> {
static inline T f(T n) { return n; }
};
template <typename T>
T rev(T n) { return RevAux<T,4*sizeof(T)>::f(n); }
int main(int argc, char *argv[])
{
unsigned long n = strtoul(argv[1],NULL,16);
printf("%lx %lx\n", n, rev(n));
}
Now, how do we check that the template parameter T is unsigned (otherwise the right shifts are probably going to go wrong)…
A simple optimization is to replace the top level function with:
template <typename T>
static inline T rev(T n) {
static const int k = 4*sizeof(T);
n = RevAux<T,k/2>::f(n);
return (n>>k)|(n<<k);
}
but GCC seems to have worked that out for itself (compiling gcc 4.4.3 , -O3 -S):
.globl _Z7reversej
pushl %ebp
movl %esp, %ebp
movl 8(%ebp), %eax
popl %ebp
movl %eax, %edx
andl $1431655765, %edx
shrl %eax
addl %edx, %edx
andl $1431655765, %eax
orl %eax, %edx
movl %edx, %eax
andl $858993459, %eax
shrl $2, %edx
andl $858993459, %edx
sall $2, %eax
orl %edx, %eax
movl %eax, %edx
andl $252645135, %edx
shrl $4, %eax
andl $252645135, %eax
sall $4, %edx
orl %eax, %edx
movl %edx, %eax
andl $16711935, %eax
shrl $8, %edx
sall $8, %eax
andl $16711935, %edx
orl %edx, %eax
rorl $16, %eax
ret
This sort of thing isn’t going to work very well if the compiler isn’t up to scratch, but GCC seems to have done it right here.
There are slightly faster ways to reverse bits using ternary swap (swap top and bottom thirds, recurse), but they need to be more ad hoc unless you have a ternary computer with word length a power of 3, so less amenable to this sort of generic treatment (or at least, it becomes a lot harder).