Excellent Numbers
Posted: January 16, 2016 Filed under: Number Theory, Python Leave a commentA number n, with an even number of digits, is excellent if it can be split into two halves, a and b, such that b2 - a2 = n. Let 2k be the number of digits, then we want n = aA + b = b2 - a2 where A = 10k.
Let’s do some algebra:
aA + b = b2 - a2
a2 + aA = b2 - b # Rearrange
4a2 + 4aA = 4b2 - 4b # Multiply by 4
(2a + A)2 - A2 = (2b - 1)2 - 1 # Complete the square
Now we can substitute X = 2a + A, Y = 2b - 1, N = A2 - 1 and rearranging a little, we have:
X2 - Y2 = N
(X - Y)(X + Y) = N
So, every 2k digit excellent number gives rise to divisors i,j of N where ij = N and i <= j
This process can be reversed: if i is a divisor of N, with j = N/i and i <= j, we have X = (j+i)/2, Y = (j-i)/2, then a = (X-A)/2 and b = (Y+1)/2. If all the divisions by 2 are exact (and in this case they are – N is odd, so i and j are too, also writing i = 2i'+1 and j = 2j'+1, we can show that i' and j' must have different parities) then we have a potentially excellent number – all we need to check is that a has exactly k digits and that b has at most k (otherwise a and b are not the upper and lower halves of a 2k digit number).
Now we have a nice algorithm: find all divisors i of N = 10k-1, with i <= sqrt(N), find a and b as above and check if they are in the appropriate range, if so, we have an excellent number and it should be clear that all excellent numbers can be generated in this way.
For small N, we can find all divisors just by a linear scan, but for larger N something better is needed: given a prime factorization we can generate all possible combinations of the factors to get the divisors, so now all we need to do is factorize 102k-1. This of course is a hard problem but we can use, for example, Python’s primefac library, and give it some help by observing that 102k-1 = (10k-1)(10k+1). The factorization is harder for some values of k, particularly if k is prime, but we can always have a look at:
http://stdkmd.com/nrr/repunit/
if we run in to trouble. My Pi 2 gets stuck at k = 71 where 11, 290249, 241573142393627673576957439049, 45994811347886846310221728895223034301839 and 31321069464181068355415209323405389541706979493156189716729115659 are the factors needed, so it’s not surprising it is struggling. Also, the number of divisors to check is approximately 2n-1 where n is the number of prime factors, of which, for example 1090-1 has 35 so just generating all potential 180 digit numbers will take a while.
So, after all that, here’s some code. Using Python generators keeps the memory usage down – we can process each divisor as it is constructed, (though it does mean that results for a particular size don’t come out in order) – after running for around 24 hours on a Pi 2, we are up to 180 digits and around 2000000 numbers but top reports less than 1% of memory in use.
import primefac
def excellent(k):
"""Generate all excellent numbers of size 2k"""
A = 10**k; N = A*A-1
factors1 = list(primefac.primefac(A-1))
factors2 = list(primefac.primefac(A+1))
d = divisors(sorted(factors1+factors2))
for i in d:
if i*i > N: continue
j = N//i
x,y = (j+i)//2, (j-i)//2
a,b = (x-A)//2, (y+1)//2
if A//10 <= a < A and 0 <= b < A:
n = a*A+b
assert(n == b*b-a*a) # Check our logic
yield n
def divisors(factorlist):
"""Generate all divisors of number from list of prime factors"""
factors = multiset(factorlist)
nfactors = len(factors)
a = [0]*nfactors; b = [1]*nfactors
yield 1
while True:
i = 0
while i < nfactors:
if a[i] < factors[i][1]: break
a[i] = 0; b[i] = 1; i += 1
if i == nfactors: break
a[i] += 1; b[i] *= factors[i][0]
for j in range(0,i): b[j] = b[i]
yield b[0]
def multiset(s):
"""Create a multiset from a (sorted) list of items"""
m = []; n = s[0]; count = 1
for i in range(1,len(s)):
if s[i] != n:
m.append((n,count))
n = s[i]
count = 1
else:
count += 1
m.append((n,count))
return m
for n in range(2,1000,2):
for m in excellent(n//2): print m
The counts for numbers up to 10100:
2: count = 1 factors = [3, 3, 11] 4: count = 1 factors = [3, 3, 11, 101] 6: count = 8 factors = [3, 3, 3, 7, 11, 13, 37] 8: count = 3 factors = [3, 3, 11, 73, 101, 137] 10: count = 3 factors = [3, 3, 11, 41, 271, 9091] 12: count = 13 factors = [3, 3, 3, 7, 11, 13, 37, 101, 9901] 14: count = 2 factors = [3, 3, 11, 239, 4649, 909091] 16: count = 3 factors = [3, 3, 11, 17, 73, 101, 137, 5882353] 18: count = 28 factors = [3, 3, 3, 3, 7, 11, 13, 19, 37, 52579, 333667] 20: count = 15 factors = [3, 3, 11, 41, 101, 271, 3541, 9091, 27961] 22: count = 9 factors = [3, 3, 11, 11, 23, 4093, 8779, 21649L, 513239L] 24: count = 51 factors = [3, 3, 3, 7, 11, 13, 37, 73, 101, 137, 9901, 99990001] 26: count = 5 factors = [3, 3, 11, 53, 79, 859, 265371653, 1058313049] 28: count = 17 factors = [3, 3, 11, 29, 101, 239, 281, 4649L, 909091L, 121499449] 30: count = 435 factors = [3, 3, 3, 7, 11, 13, 31, 37, 41, 211, 241, 271, 2161, 9091, 2906161] 32: count = 157 factors = [3, 3, 11, 17, 73, 101, 137, 353, 449, 641, 1409, 69857, 5882353] 34: count = 4 factors = [3, 3, 11, 103, 4013L, 2071723L, 5363222357L, 21993833369L] 36: count = 66 factors = [3, 3, 3, 3, 7, 11, 13, 19, 37, 101, 9901L, 52579L, 333667L, 999999000001L] 38: count = 2 factors = [3, 3, 11, 909090909090909091L, 1111111111111111111L] 40: count = 103 factors = [3, 3, 11, 41, 73, 101, 137, 271, 3541L, 9091L, 27961L, 1676321L, 5964848081L] 42: count = 999 factors = [3, 3, 3, 7, 7, 11, 13, 37, 43, 127, 239, 1933L, 2689L, 4649L, 459691L, 909091L, 10838689L] 44: count = 89 factors = [3, 3, 11, 11, 23, 89, 101, 4093L, 8779L, 21649L, 513239L, 1052788969L, 1056689261L] 46: count = 2 factors = [3, 3, 11, 47, 139, 2531L, 549797184491917L, 11111111111111111111111L] 48: count = 188 factors = [3, 3, 3, 7, 11, 13, 17, 37, 73, 101, 137, 9901L, 5882353L, 99990001L, 9999999900000001L] 50: count = 45 factors = [3, 3, 11, 41, 251, 271, 5051L, 9091L, 21401L, 25601L, 182521213001L, 78875943472201L] 52: count = 11 factors = [3, 3, 11, 53, 79, 101, 521, 859, 265371653L, 1058313049L, 1900381976777332243781L] 54: count = 150 factors = [3, 3, 3, 3, 3, 7, 11, 13, 19, 37, 757, 52579L, 333667L, 70541929L, 14175966169L, 440334654777631L] 56: count = 99 factors = [3, 3, 11, 29, 73, 101, 137, 239, 281, 4649L, 7841L, 909091L, 121499449L, 127522001020150503761L] 58: count = 2 factors = [3, 3, 11, 59, 3191L, 16763L, 43037L, 62003L, 77843839397L, 154083204930662557781201849L] 60: count = 35929 factors = [3, 3, 3, 7, 11, 13, 31, 37, 41, 61, 101, 211, 241, 271, 2161L, 3541L, 9091L, 9901L, 27961L, 2906161L, 4188901L, 39526741L] 62: count = 2 factors = [3, 3, 11, 2791L, 6943319L, 57336415063790604359L, 909090909090909090909090909091L] 64: count = 1162 factors = [3, 3, 11, 17, 73, 101, 137, 353, 449, 641, 1409L, 19841L, 69857L, 976193L, 5882353L, 6187457L, 834427406578561L] 66: count = 478 factors = [3, 3, 3, 7, 11, 11, 13, 23, 37, 67, 4093L, 8779L, 21649L, 513239L, 599144041L, 183411838171L, 1344628210313298373L] 68: count = 28 factors = [3, 3, 11, 101, 103, 4013L, 2071723L, 28559389L, 1491383821L, 5363222357L, 21993833369L, 2324557465671829L] 70: count = 146 factors = [3, 3, 11, 41, 71, 239, 271, 4649L, 9091L, 123551L, 909091L, 4147571L, 102598800232111471L, 265212793249617641L] 72: count = 3627 factors = [3, 3, 3, 3, 7, 11, 13, 19, 37, 73, 101, 137, 3169L, 9901L, 52579L, 98641L, 333667L, 99990001L, 999999000001L, 3199044596370769L] 74: count = 4 factors = [3, 3, 11, 7253L, 2028119L, 247629013L, 422650073734453L, 296557347313446299L, 2212394296770203368013L] 76: count = 5 factors = [3, 3, 11, 101, 722817036322379041L, 909090909090909091L, 1111111111111111111L, 1369778187490592461L] 78: count = 700 factors = [3, 3, 3, 7, 11, 13, 13, 37, 53, 79, 157, 859, 6397L, 216451L, 265371653L, 1058313049L, 388847808493L, 900900900900990990990991L] 80: count = 605 factors = [3, 3, 11, 17, 41, 73, 101, 137, 271, 3541L, 9091L, 27961L, 1676321L, 5070721L, 5882353L, 5964848081L, 19721061166646717498359681L] 82: count = 2 factors = [3, 3, 11, 83, 1231L, 538987L, 2670502781396266997L, 3404193829806058997303L, 201763709900322803748657942361L] 84: count = 59490 factors = [3, 3, 3, 7, 7, 11, 13, 29, 37, 43, 101, 127, 239, 281, 1933L, 2689L, 4649L, 9901L, 226549L, 459691L, 909091L, 10838689L, 121499449L, 4458192223320340849L] 86: count = 9 factors = [3, 3, 11, 173, 1527791L, 57009401L, 2182600451L, 1963506722254397L, 2140992015395526641L, 7306116556571817748755241L] 88: count = 105 factors = [3, 3, 11, 11, 23, 73, 89, 101, 137, 617, 4093L, 8779L, 21649L, 513239L, 1052788969L, 1056689261L, 16205834846012967584927082656402106953L] 90: count = 50344 factors = [3, 3, 3, 3, 7, 11, 13, 19, 31, 37, 41, 211, 241, 271, 2161L, 9091L, 29611L, 52579L, 238681L, 333667L, 2906161L, 3762091L, 8985695684401L, 4185502830133110721L] 92: count = 26 factors = [3, 3, 11, 47, 101, 139, 1289L, 2531L, 18371524594609L, 549797184491917L, 11111111111111111111111L, 4181003300071669867932658901L] 94: count = 2 factors = [3, 3, 11, 6299L, 35121409L, 4855067598095567L, 297262705009139006771611927L, 316362908763458525001406154038726382279L] 96: count = 80002 factors = [3, 3, 3, 7, 11, 13, 17, 37, 73, 97, 101, 137, 353, 449, 641, 1409L, 9901L, 69857L, 206209L, 5882353L, 99990001L, 66554101249L, 75118313082913L, 9999999900000001L] 98: count = 10 factors = [3, 3, 11, 197, 239, 4649L, 909091L, 505885997L, 1976730144598190963568023014679333L, 5076141624365532994918781726395939035533L] 100: count = 3573 factors = [3, 3, 11, 41, 101, 251, 271, 3541L, 5051L, 9091L, 21401L, 25601L, 27961L, 60101L, 7019801L, 182521213001L, 14103673319201L, 78875943472201L, 1680588011350901L]
Time to generate that lot, about 3m30s on my Core I3 laptop, about 30m on my Raspberry Pi 2.
Finally, if we want really big numbers, then we don’t need a full factorization – http://stdkmd.com/nrr/repunit/ has enough factors of 102016-1, for example, to find, among others:
467203616037752709753640875404905278610286278867781588976105221346970432 395736683257666616868811083043941463314513845761368180251295614288295272 712974920189045619317506423133721608367014923830041699210760183164585217 599174938750569917513095900320978144876083087591215818424979192187341459 756509047543186958692244904217361382312220589759551138455399864423950556 877618463844146927376784311673205223822619959320039184981861810037019868 259785305305318574127400789513920685551635257636719954377249042716215901 383844447790548649266546486400561808622649593166435681150190744136685886 335659851446510906275097594875425811830427470257238967118169107518206073 615596540306297513679739458887733205329861379807932402155440131595447258 905459620119681006553819769296088325096562295835757909167184772591564873 889571115660015460170065915133627063917081464432904541564462471704065596 995864597351005042459541065531684772723537478273137238536882143270837967 355784692820692700257668090096174851711901872379544776234666991080481050 827938907695794044434449897483410036041789283630321915114061710879582491 425436499562245749681317500307257068229179611956588865266983050266693593 782449462829670744802988126608915433835744545694648340583599198978087691 600147477867595689158751559170609174089828925445708502246431435332615649 355141085750085715940292846105899585176839916452603275591677348739914677 778216128911941208439459006047576543241292648992222090990416741035195043 278539082418243317317374583211686841192215307443355453487377377290350196 371354628663013301973808912217716856093563005467214390853254407353722627 416963492751125708925240306094459245276161787679224919637918913006752210 513662791886758732646236407566089976349268846643228836678505302621204788 560791609138040737880910308235667105956827669559476643173829425259196119 155907391268256981917731226756506952400793923896521065760681749285568778 344719401424538913519492510286853888028737195080140956569785690813785590 037948199410250551049984142378021668001361835139075663440830359075663125
Which should be enough excellence for anybody. If not, https://www.dropbox.com/s/9xdnxd0ifla0zhf/excellent100.txt.gz has a list of all numbers up to 100 digits.
0 1 1 2 3 5 8 13…
Posted: January 1, 2013 Filed under: Number Theory, Python Leave a commentFor some reason I spent some time over Christmas looking at algorithms for computing Fibonacci numbers, so here’s the first post for 2013.
The Binet formulas for the Fibonacci and Lucas numbers are:
φ = (1+√5)/2
ψ = (1-√5)/2
φψ = -1
Fn = (φn-ψn)/√5
Ln = φn+ψn
We can now derive:
5Fn2 = φ2n+ψ2n-2(-1)n = L2n-2(-1)n
Ln2 = φ2n+ψ2n+2(-1)n = L2n+2(-1)n
LnFn = (φ2n-ψ2n)/5 = F2n
We can also use the formulas to prove:
2φn = Ln + Fn√5
which gives us:
Ln+m + Fn+m√5 = 2φn+m = 2φnφm = (LnLm+5FnFm)/2 + (LnFm+FnLm)√/2
So, equating the rational and irrational parts (as we may – if a+bk = c+dk with a,b,c,d rational, then k is rational unless a=c and b=d):
Ln+m = (LnLm+5FnFm)/2
Fn+m = (LnFm+FnLm)/2
Two special cases for this:
L2n = (Ln2+5Fn2)/2
F2n = LnFn
Ln+1 = (Ln+5Fn)/2
Fn+1 = (Ln+Fn)/2
With these recurrences, we can write some code:
def fib1aux(n):
"""Return F(n),L(n)"""
if n == 0: return 0,2
else:
a,b = fib1aux(n//2)
a,b = a*b,(5*a*a+b*b)//2
if n%2 == 0: return a,b
else: return (a+b)//2, (5*a+b)//2
return a,b
def fib1(n): return fib1aux(n)[0]
We can save a bignum multiplication in each recursive step by replacing a,b = a*b,(5*a*a+b*b)//2 with something like ab = a*b; t = (a+b)*(5*a+b); a,b = ab,t//2-3*ab (suggestion due to Robin Houston at http://bosker.wordpress.com/2011/07/27/computing-fibonacci-numbers-using-binet%E2%80%99s-formula/).
Alternatively, we can follow the suggestion of Knuth in TAOCP (solution to exercise 4.6.3.26) and define:
def fib2aux(n):
"""Return F(n),L(n)"""
if n == 0: return 0,2
else:
a,b = fib2aux(n//2)
a,b = a*b,n//2%2*4-2+b*b
if n%2 == 0: return a,b
else: return (a+b)//2, (5*a+b)//2
def fib2(n): return fib2aux(n)[0]
In both cases, we benefit from avoiding the final calculation of Ln and define something like:
def fib2(n):
if (n%2 == 0):
a,b = fib2aux(n//2)
return a*b
else:
a,b = fib2aux(n-1)
return (a+b)//2
or, for a non-recursive solution (stealing some ideas from Robin Houston again):
def bits(n):
r = []
while n!=0:
r.append(n%2)
n >>=1
r.reverse()
return r
def fib3(n):
a,b = 0,2
last = 0
for i in bits(n//2):
a,b = a*b,last*4-2+b*b
last = i
if i: a,b = (a+b)//2, (5*a+b)//2
if n%2 == 0:
return a*b
else:
a,b = a*b,last*4-2+b*b
return (a+b)//2
Of course, we don’t have to use Lucas numbers, a pleasant recurrence for Fibonacci numbers alone is:
Fn+m = Fn+1Fm+FnFm-1
which gives us:
F2n = FnFn+2FnFn-1
F2n-1 = FnFn+Fn-1Fn-1
and
F2n+1 = Fn+1Fn+1+FnFn
F2n = 2FnFn+1-FnFn
leading to:
def fibaux4(n):
if n == 0: return 0,1
elif n == 1: return 1,0
else:
a,b = fibaux4((n+1)//2)
if (n%2 == 0): return a*(a+2*b),a*a+b*b
else: return a*a+b*b,b*(2*a-b)
def fib4(n): return fibaux4(n)[0]
with an elegant symmetry between the odd and even cases. This seems to be solution suggested by Dijkstra in http://www.cs.utexas.edu/~EWD/ewd06xx/EWD654.PDF.
There is, of course more: notably the matrix based solutions – we observe that (an+2,an+1) is M(an+1,an) for 2×2 matrix M = (1 1 1 0). We then have (Fn+1,Fn) = Mn(1 0) and we can use conventional matrix operations, including inversion, to compute Fn. We can apply this to any linear recurrence, eg. an+2 = Aan+1+Ban corresponds to the matrix (A B 1 0).
It’s notable that M only depends on the recurrence and not on the initial values, so we can compute, for example, the Lucas numbers with (Ln+1,Ln) = Mn(1 2), and there is a regularity to the structure of M that can be used to optimise the computation, eg. for Fibonacci, M is of the form (a+b a a b) (cf. HAKMEM: http://www.inwap.com/pdp10/hbaker/hakmem/recurrence.html). But that probably needs another post.
Complex Fibonacci
Posted: December 22, 2012 Filed under: Floating Point, Number Theory Leave a comment
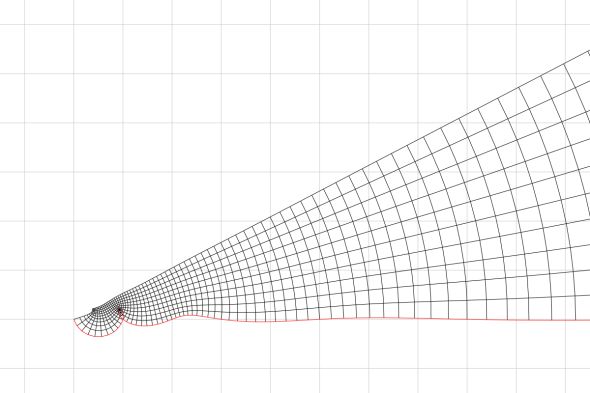
There are a couple of ways to extend the Fibonacci series to a continuous function on real or complex numbers. Here’s a nice one: the grid shows the mapping of the unit strip, 0 <= re(z), 0 <= im(z) <= 1, grid points are 0.1 apart. The real axis is picked out in red, notice that it crosses itself exactly at the points of the Fibonacci series – twice at 1 after executing a loop-the-loop (clicking on the image should give you a larger version).
The function is just the standard Binet formula, interpreted over the complex plane:
(φz - -φ-z)/√5
or equivalently:
(φz - eiπzφ-z)/√5
For negative values, the function turns into a nice spiral (the exp component dominates). Here is the 0 <= im(z) <= 0.1 strip:
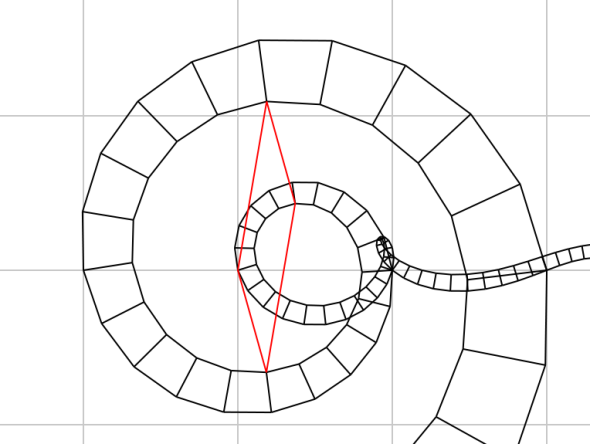
The red parallelogram illustrates F(z+2) = F(z+1)+F(z) still holds, even for our complex quantities.
Most of the action takes place around the origin, so let’s zoom in:
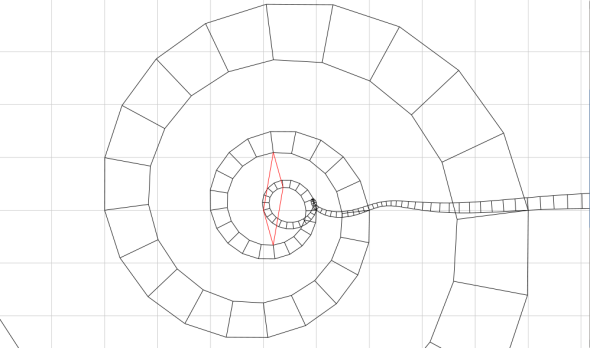
The image of the real axis passing through the points -1,1,0,1,1,2,… is clearly visible (the real axis is on the outside, the origin is the leftmost point on the red parallelogram).
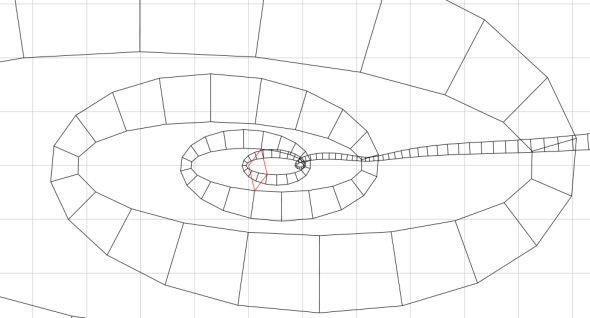
Sometimes the series is extended as (φz - cos(πz)φ-z)/√5 which produces a mapping that takes the real line to itself, ie. taking the real part of the exponential, which is also nice, here we see the mapping of the strip 0.1 <= im(z) <= 0.2:
Again, the red parallelogram illustrates the recurrence.